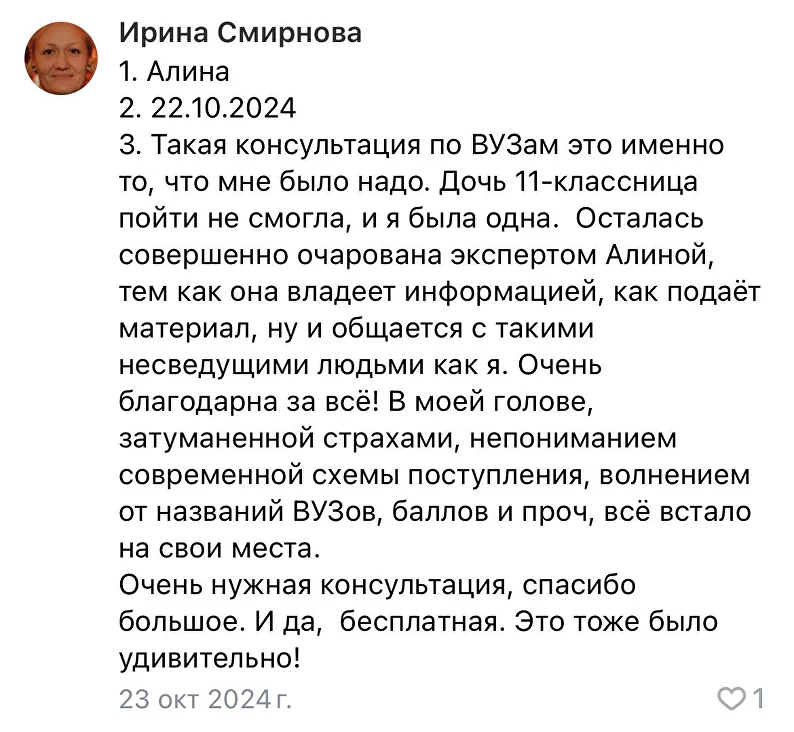
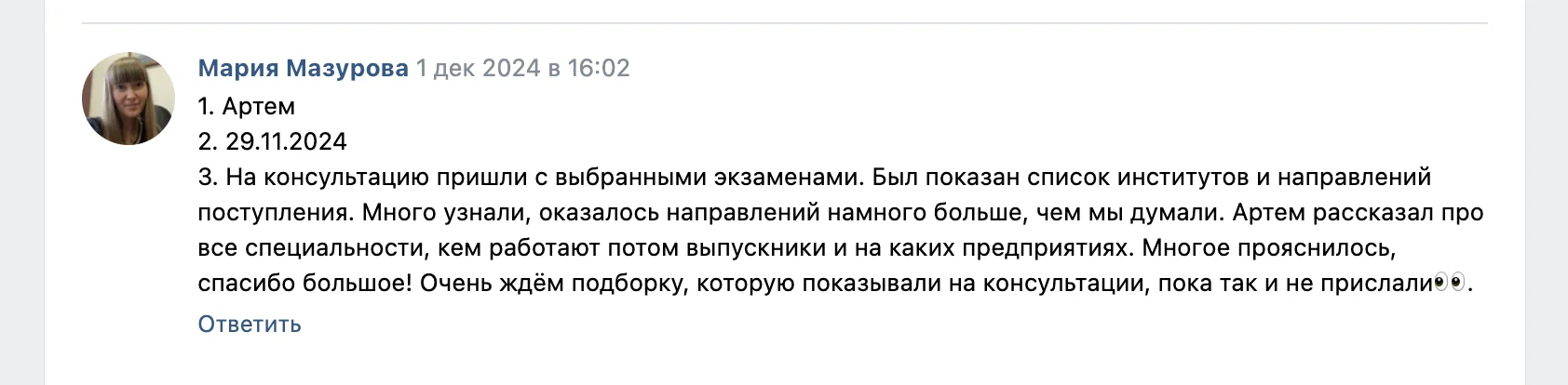
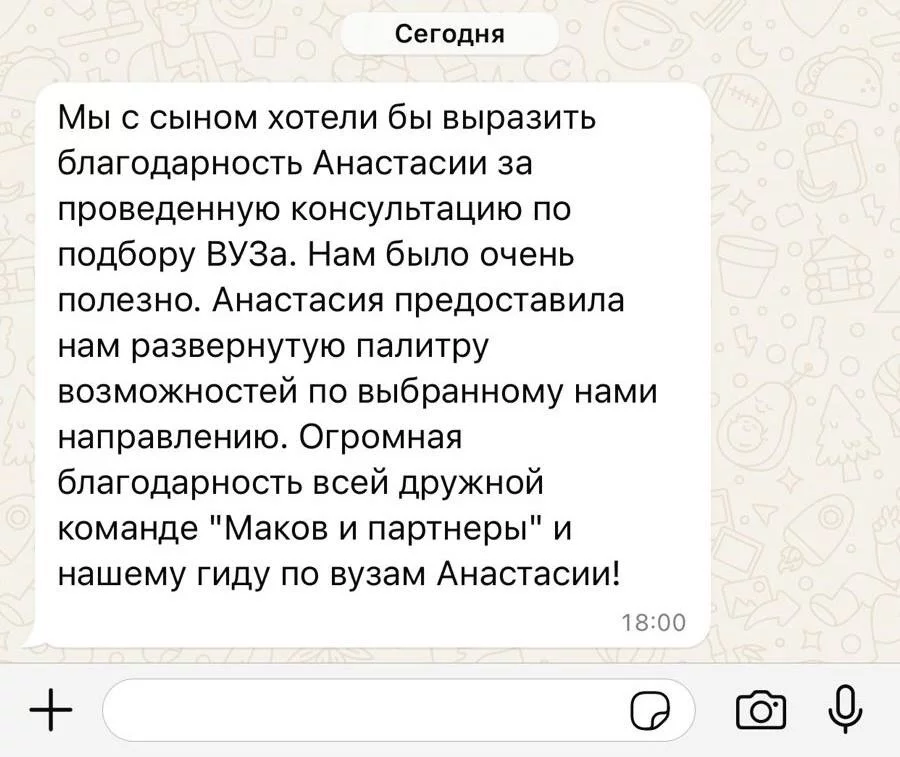
Привет! Я Эрнест, самый топовый преподаватель по математике ;)
Сегодня узнаешь, почему нельзя делить на ноль и можно ли все-таки попробовать?
Что такое деление?
Деление – это операция обратная умножению. Для натуральных чисел деление
обозначает нахождение, какое число надо взять столько-то раз, чтобы получилось
данное.
Например, 12 : 3 = n, n – такое число, которое при умножении на 3 дает 12.
Другой пример, 40 : 8 = k, k – такое число, которое при умножении на 8 дает 40.
Почему на 0 делить нельзя?
Из правил, которые мы вывели в предыдущем пункте, мы можем сказать, что
1: 0 = n, 1 = n*0,
Но ведь мы знаем, что любое число, умноженное на ноль — это ноль. Значит, это тождество неверно. Можно подумать, что 0 : 0 = m, 0 = m*0. Это уравнение уже имеет решение. Проблема в том, что у него очень много решений. Выражение 0:0 не имеет смысла, потому что оно имеет бесконечно много решений.
Почему все решили, что на 0 делить можно
Многие старшеклассники либо студенты, узнав, что такое предел, увидели подобную запись: lim (1/х) = ∞, где х → 0. В конце концов предел стремится к нулю, и они решили, что в конце концов 1/0 = ∞. Тогда получается 1 = ∞*0. Но логично, что это не так, потому что нет такого числа, которое при умножении на 0 дает что-то отличное от нуля. В целом в данном случае возникает подмена понятий бесконечность – не
число. Бесконечность – это символ, который обозначает что-то, что больше всех чисел, но использовать ее в числовых вычислениях нельзя.
Почему иногда можно делить на 0
На первом курсе вам расскажут, что такое предел, как с ним работать. И тогда вы поймете, что в математическом анализе знаком 0 обозначают не совсем нуль. Знаком 0 обозначают такое число, которое очень сильно близится к нулю, но его не достигает. Поэтому по- хорошему запись 1/0 = ∞ должна выглядеть так:
Эта запись читается так: если существует последовательность, которая стремиться к нулю, но ни один член последовательности не равен нулю, тогда предел последовательности 1/Xn = ∞. НО! Обратите
внимание на то, что у равенства (1) есть условие, что Xn ≠ 0. Это происходит как
раз из-за того, что на нуль делить нельзя.
Мы можем прийти к выводу, что на 0 делить нельзя ни при каком исходе. Это неверно. И когда в школе говорят, что на 0 делить нельзя, вас не обманывают, это действительно так. Вам никто не откроет какого-то секретного знания, где окажется, что делить на 0 можно. К сожалению, такого быть не может.
Жду тебя на курсах по профилю в Макове ;)
Сегодня узнаешь, почему нельзя делить на ноль и можно ли все-таки попробовать?
Что такое деление?
Деление – это операция обратная умножению. Для натуральных чисел деление
обозначает нахождение, какое число надо взять столько-то раз, чтобы получилось
данное.
Например, 12 : 3 = n, n – такое число, которое при умножении на 3 дает 12.
Другой пример, 40 : 8 = k, k – такое число, которое при умножении на 8 дает 40.
Почему на 0 делить нельзя?
Из правил, которые мы вывели в предыдущем пункте, мы можем сказать, что
1: 0 = n, 1 = n*0,
Но ведь мы знаем, что любое число, умноженное на ноль — это ноль. Значит, это тождество неверно. Можно подумать, что 0 : 0 = m, 0 = m*0. Это уравнение уже имеет решение. Проблема в том, что у него очень много решений. Выражение 0:0 не имеет смысла, потому что оно имеет бесконечно много решений.
Почему все решили, что на 0 делить можно
Многие старшеклассники либо студенты, узнав, что такое предел, увидели подобную запись: lim (1/х) = ∞, где х → 0. В конце концов предел стремится к нулю, и они решили, что в конце концов 1/0 = ∞. Тогда получается 1 = ∞*0. Но логично, что это не так, потому что нет такого числа, которое при умножении на 0 дает что-то отличное от нуля. В целом в данном случае возникает подмена понятий бесконечность – не
число. Бесконечность – это символ, который обозначает что-то, что больше всех чисел, но использовать ее в числовых вычислениях нельзя.
Почему иногда можно делить на 0
На первом курсе вам расскажут, что такое предел, как с ним работать. И тогда вы поймете, что в математическом анализе знаком 0 обозначают не совсем нуль. Знаком 0 обозначают такое число, которое очень сильно близится к нулю, но его не достигает. Поэтому по- хорошему запись 1/0 = ∞ должна выглядеть так:
lim Xn = 0 (Xn ≠ 0) (1)
lim 1/Хn = ∞ (2)
Эта запись читается так: если существует последовательность, которая стремиться к нулю, но ни один член последовательности не равен нулю, тогда предел последовательности 1/Xn = ∞. НО! Обратите
внимание на то, что у равенства (1) есть условие, что Xn ≠ 0. Это происходит как
раз из-за того, что на нуль делить нельзя.
Мы можем прийти к выводу, что на 0 делить нельзя ни при каком исходе. Это неверно. И когда в школе говорят, что на 0 делить нельзя, вас не обманывают, это действительно так. Вам никто не откроет какого-то секретного знания, где окажется, что делить на 0 можно. К сожалению, такого быть не может.
Жду тебя на курсах по профилю в Макове ;)